|
The
design of acoustooptic tunable filters is one of the most discussed problems
in present acoustooptics because of a very wide area of the application
of these devices in quantum electronics, spectrometry and spectropolarimetry,
fluorescence spectroscopy, spectral imaging , telecommunication etc.
The
principle of operation of the filters is based on the dependence of the
diffracttted light wavelength on the acoustic frequency. There are two types
of the acoustooptic filters – collinear and non-collinear filters – depending
on geometry of acoustooptic interaction. Here we consider only non-collinear
filters based on the TeO2 single crystal. A basic geometry
of the acoustooptic interaction in the filter is shown in Fig. 1f. The
polarization of the incident light can be either ordinary or extraordinary.
For the definition, we assume ordinary polarization. Here the following
system of symbols is used:
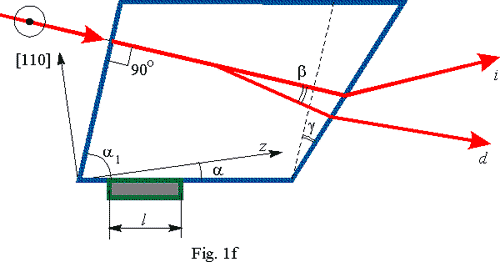
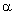 is the angle between
the acoustic wave vector and the crystallographic axis z
of the crystal; is the angle between
the acoustic wave vector and the crystallographic axis z
of the crystal;
 is the wedge angle
between the input and output faces of the filter cell (the wedge angle
is necessary for eliminating the angular shift of the diffracttted beam
caused by frequency changing); is the wedge angle
between the input and output faces of the filter cell (the wedge angle
is necessary for eliminating the angular shift of the diffracttted beam
caused by frequency changing);
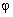 is the angle between
the incident light wave vector and [110] axis of the crystal; is the angle between
the incident light wave vector and [110] axis of the crystal;
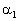 is the angle between
the input face of the cell and acoustic wave vector; is the angle between
the input face of the cell and acoustic wave vector;
 is the angle between
deflected and non-deflected light at the central frequency; is the angle between
deflected and non-deflected light at the central frequency;
l
is the transducer length.
The
incidence angle  and the central frequency and the central frequency
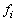 of the filter is defined
by the following set of equations: of the filter is defined
by the following set of equations:
 |
(1f) |
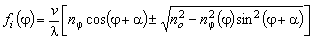 |
(2f) |
Indices
of refraction for ordinary (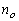 ) and extraordinary ( ) and extraordinary ( ) polarized beams are
determined with taking into account their dispersive dependence. ) polarized beams are
determined with taking into account their dispersive dependence.
The
sound velocity v depends on the angle 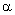
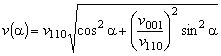 |
(3f) |
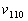 and and 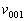 are the sound velocities
along the axes [110] and [001], correspondingly. The value of are the sound velocities
along the axes [110] and [001], correspondingly. The value of 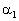 is determined by the
angles is determined by the
angles 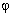 and and 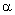
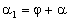 |
(4f) |
The
angle 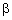 between the diffracttted
and non-diffracttted beams defines the view field of the filter; it can
be calculated from the formula between the diffracttted
and non-diffracttted beams defines the view field of the filter; it can
be calculated from the formula
 |
(5f) |
Basic
parameters of the filter are spectral resolution  and spectral tuning
band and spectral tuning
band  . The spectral resolution
at 3 dB level is determined from the expression . The spectral resolution
at 3 dB level is determined from the expression
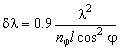 |
(6f) |
The
tuning band  is defines by the
frequency band of the transducer. As a rule, the band does not exceed
octave, especially in UV region of the spectrum. Here we present characteristics
of a row of the filters which cover the optical region from UV to IR:
550-900 nm, 900-1800 nm and 1800-4000. is defines by the
frequency band of the transducer. As a rule, the band does not exceed
octave, especially in UV region of the spectrum. Here we present characteristics
of a row of the filters which cover the optical region from UV to IR:
550-900 nm, 900-1800 nm and 1800-4000.
|