| |
Acousto-optic effect, also known in the scientific literature
as acousto-optic interaction or diffraction of light by acoustic waves,
was first predicted by Brillouin in 1921 and experimentally revealed by
Lucas, Biquard and Debye, Sears in 1932.
The basis of the acousto-optic interaction is a more
general effect of photoelasticity consisting in the change of the medium
permittivity 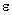 under the action of
a mechanical strain a. Phenomenologically, this effect is described
as variations of the optical indicatrix coefficients under the action of
a mechanical strain a. Phenomenologically, this effect is described
as variations of the optical indicatrix coefficients 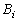 caused by the strain caused by the strain
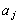 : :
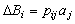 |
(1) |
 where where 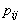 is the photoelastic tensor components, i,j = 1,2,…,6.
In case of the acousto-optic effect, the strains
is the photoelastic tensor components, i,j = 1,2,…,6.
In case of the acousto-optic effect, the strains 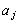 are produced by an acoustic wave excited in a transparent medium. Thus,
one can say that the acoustic wave is accompanied by a wave of refractive
index variations. For a plane acoustic wave propagating along the axis z,
one can write that
are produced by an acoustic wave excited in a transparent medium. Thus,
one can say that the acoustic wave is accompanied by a wave of refractive
index variations. For a plane acoustic wave propagating along the axis z,
one can write that
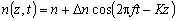 , , |
(2) |
where n
is the undisturbed index of refraction, f
and K are the frequency and propagation
constant of the acoustic wave, 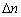 is the amplitude variation
of the refractive index induced by the acoustic wave: is the amplitude variation
of the refractive index induced by the acoustic wave:
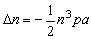 . . |
(3) |
For the light, the medium with the refraction index (2) represents a phase
grating moving with the sound velocity v.
Passing the medium, the light diffracts on inhomogeneities of the refraction
index, forming in the far field a salient diffraction pattern.
On examination of light diffraction by a monochromatic acoustic wave,
two limiting regimes are distinguished first of all – the regimes of Raman-Nath
and Bragg. The Raman-Nath regime is observed at relatively low acoustic
frequencies f and a small acoustooptic interaction length
l (typically, f < 10MHz and l < 1cm). This type of diffraction takes
place at an arbitrary incidence angle of light 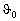 (Fig. 1,a). The diffraction pattern can contain many
diffraction orders with symmetrical distribution of light intensity. By
contrast, the Bragg regime is observed at high acoustic frequencies exceeding
usually 100MHz. The diffraction pattern, even at a large acoustic power (Fig. 1,a). The diffraction pattern can contain many
diffraction orders with symmetrical distribution of light intensity. By
contrast, the Bragg regime is observed at high acoustic frequencies exceeding
usually 100MHz. The diffraction pattern, even at a large acoustic power
 , consists, as a rule, of
two diffraction maxima of the zeroth and first orders. , consists, as a rule, of
two diffraction maxima of the zeroth and first orders.
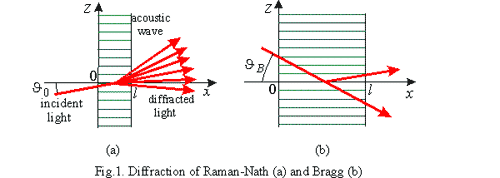 |
However,
even these maxima appear only at definite incidence angles near the so-called
Bragg angle  (Fig. 1,b). In this case, the side maximum (Bragg maximum) is formed as
a selective reflection of light from wave fronts of ultrasound. The Bragg
angle is determined by the expression
(Fig. 1,b). In this case, the side maximum (Bragg maximum) is formed as
a selective reflection of light from wave fronts of ultrasound. The Bragg
angle is determined by the expression
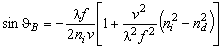 , , |
(4) |
where 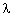 is the optical wavelength
in vacuum, is the optical wavelength
in vacuum, 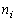 and and 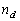 are the refraction indices
for the incident and diffracted light, respectively.
There is no well-defined boundary between these two diffraction regimes.
With increasing the acoustic frequency the angular selectivity of acousto-optic
interaction increases and the number of observed maxima is gradually reduced.
Traditionally, the Raman-Nath and Bragg regimes are stated by the conditions
Q << 1 and Q >> 1 accordingly, where are the refraction indices
for the incident and diffracted light, respectively.
There is no well-defined boundary between these two diffraction regimes.
With increasing the acoustic frequency the angular selectivity of acousto-optic
interaction increases and the number of observed maxima is gradually reduced.
Traditionally, the Raman-Nath and Bragg regimes are stated by the conditions
Q << 1 and Q >> 1 accordingly, where 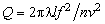 is the Klein-Cook parameter. Since only one diffraction
maximum is used in acousto-optic devices (the first order, as a rule), the
Bragg regime is more preferable because of smaller light losses. However,
the acousto-optic selectivity peculiar to the Bragg diffraction restricts
the frequency range of acousto-optic interaction and, as a consequence,
speed of operation of acousto-optic devices. If the acoustooptic
medium is optically isotropic, then is the Klein-Cook parameter. Since only one diffraction
maximum is used in acousto-optic devices (the first order, as a rule), the
Bragg regime is more preferable because of smaller light losses. However,
the acousto-optic selectivity peculiar to the Bragg diffraction restricts
the frequency range of acousto-optic interaction and, as a consequence,
speed of operation of acousto-optic devices. If the acoustooptic
medium is optically isotropic, then 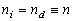 and Eq. (4) is simplified to and Eq. (4) is simplified to
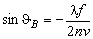 . . |
(5) |
Curve 1 in Fig. 2 shows the dependence 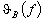 for this case. In an anisotropic
medium, two types of acousto-optic interaction are possible. If the optical
mode does not change during the acousto-optic interaction, then for this case. In an anisotropic
medium, two types of acousto-optic interaction are possible. If the optical
mode does not change during the acousto-optic interaction, then 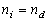 ( (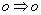 type of scattering) or type of scattering) or
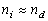 ( (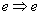 scattering) and the Bragg
angle is determined by Eq. (5). This type of acousto-optic interaction is
known as isotropic diffraction. In the other case known as anisotropic diffraction,
the optical mode is transformed during the diffraction process ( scattering) and the Bragg
angle is determined by Eq. (5). This type of acousto-optic interaction is
known as isotropic diffraction. In the other case known as anisotropic diffraction,
the optical mode is transformed during the diffraction process (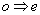 or or 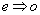 scattering). Therefore, scattering). Therefore,
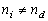 and the dependence and the dependence 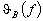 becomes much more complicated.
Curves 2 and 3 in Fig. 2 demonstrate these dependencies for
a relatively simple variant when the acousto-optic interaction plane is
perpendicular to the optical axis of an uniaxial crystal. From the viewpoint
of practical usage, all advantages of anisotropic diffraction result from
these complicated dependences of the Bragg angle on the acoustic frequency.
It has been shown that the best characteristics of acousto-optic deflectors
are achieved in the region where becomes much more complicated.
Curves 2 and 3 in Fig. 2 demonstrate these dependencies for
a relatively simple variant when the acousto-optic interaction plane is
perpendicular to the optical axis of an uniaxial crystal. From the viewpoint
of practical usage, all advantages of anisotropic diffraction result from
these complicated dependences of the Bragg angle on the acoustic frequency.
It has been shown that the best characteristics of acousto-optic deflectors
are achieved in the region where 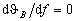 (point d in Fig.2).
Analogously, optimal areas for modulators and filters are situated close
to points m and f, (point d in Fig.2).
Analogously, optimal areas for modulators and filters are situated close
to points m and f,
 |
respectively,
where 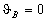 and and 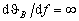 . An
analytical solution of the problem of acousto-optic interaction can be obtained
only for the limiting cases of Raman-Nath and Bragg diffraction. In the
latter case, assuming additionally that the optical beam falls on the acousto-optic
cell at the Bragg angle, the following expression for the diffraction efficiency
can be derived: . An
analytical solution of the problem of acousto-optic interaction can be obtained
only for the limiting cases of Raman-Nath and Bragg diffraction. In the
latter case, assuming additionally that the optical beam falls on the acousto-optic
cell at the Bragg angle, the following expression for the diffraction efficiency
can be derived:
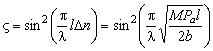 , , |
(6) |
where 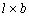 is the cross-section of
the acoustic beam. The parameter M defined by the expression is the cross-section of
the acoustic beam. The parameter M defined by the expression
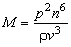 , , |
(7) |
where 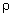 is the medium density,
is known as an acousto-optic figure of merit; it is the main parameter of
the acousto-optic medium. The greater the figure of merit, the less the
required acoustic power is the medium density,
is known as an acousto-optic figure of merit; it is the main parameter of
the acousto-optic medium. The greater the figure of merit, the less the
required acoustic power 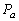 . .
|