|
Optical
deflectors are intended for spatial controlling optical beams. The functioning
of the acoustooptic deflectors is based on the dependence of the diffraction
angle 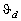 on the acoustic frequency
f: varying the frequency in the range on the acoustic frequency
f: varying the frequency in the range
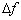 produces changing
the diffraction angle in the range produces changing
the diffraction angle in the range
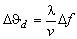 , , |
(1d) |
where 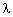 is the optical wavelength,
v is the acoustic velocity. is the optical wavelength,
v is the acoustic velocity.
The
most important characteristic of the deflector is its resolution which
is understood as a number of spatially resolved light elements (spots)
kept within the scanning line. Thus, one can define the number of resolved
elements N as a ratio of the scanning angle 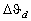 to the angular width
of the scanning beam to the angular width
of the scanning beam 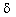 : : 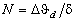 . The divergence of
the diffracted beam . The divergence of
the diffracted beam 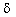 depends on the distribution
of the incident light intensity over the acoustooptic cell aperture, as
well as on the resolution criterion. It is a common practice to use the
Rayleigh criterion, according to which two spots of equal intensity are
considered resolved, if the total intensity between the two spots is 81%
of that at the centres of the spots. In this case depends on the distribution
of the incident light intensity over the acoustooptic cell aperture, as
well as on the resolution criterion. It is a common practice to use the
Rayleigh criterion, according to which two spots of equal intensity are
considered resolved, if the total intensity between the two spots is 81%
of that at the centres of the spots. In this case 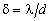 , where d
is the linear optical aperture in the acoustooptic interaction plane.
As a result, one can yield the following expression: , where d
is the linear optical aperture in the acoustooptic interaction plane.
As a result, one can yield the following expression:
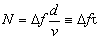 . . |
(2d) |
This
relationship shows that for a given material the resolution is proportional
to the cell aperture and to the acoustic frequency bandwidth. The parameter
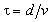 determines the time
required for the ultrasound to cross the optical beam. In essence, determines the time
required for the ultrasound to cross the optical beam. In essence, 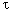 is the switching time
or the response time of the device upon a discrete change of the sound
frequency. is the switching time
or the response time of the device upon a discrete change of the sound
frequency.
Below
we consider acoustooptic deflectors based on TeO2 single crystals.
Such deflectors employ so-called anisotropic diffraction of light. This
type of acoustooptic interaction is much more complicated than isotropic
diffraction. A number of deflector parameters cannot be found in analytical
formulae and arduous numerical calculations are required.
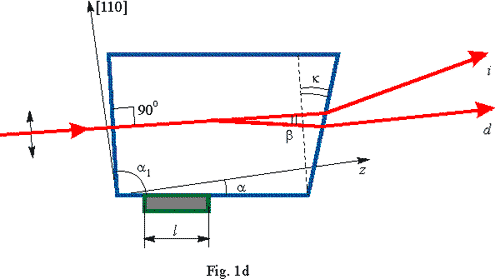
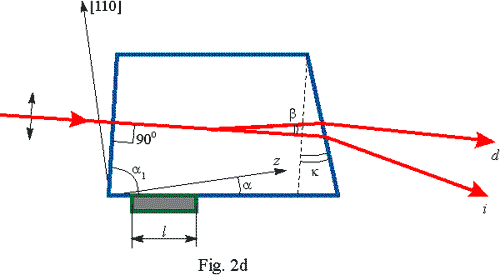
The
basic geometry of the acoustooptic deflector is presented in Figs 1d and
2d. The geometry shown in Fig. 1d is more preferable for the visible region,
whereas the geometry displayed in Fig. 2d is more suitable for the infrared
region. Polarization of the incident light is shown in the figures. Here
the following system of symbols is used:
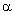 is the angle between
the acoustic wave vector and the crystallographic axis z
of the crystal; is the angle between
the acoustic wave vector and the crystallographic axis z
of the crystal;
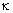 is the wedge angle
between the input and output faces of the deflector cell (the wedge angle
is necessary for to keep the direction of the scanning beam at the central
frequency collinearly to the direction of the incident beam); is the wedge angle
between the input and output faces of the deflector cell (the wedge angle
is necessary for to keep the direction of the scanning beam at the central
frequency collinearly to the direction of the incident beam);
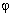 is the angle between
the incident light wave vector and [110] axis of the crystal; is the angle between
the incident light wave vector and [110] axis of the crystal;
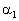 is the angle between
the input face of the cell and acoustic wave vector; is the angle between
the input face of the cell and acoustic wave vector;
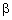 is the angle between
deflected and non-deflected light at the central frequency; is the angle between
deflected and non-deflected light at the central frequency;
l
is the transducer length.
The
incidence angle 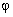 and the central frequency and the central frequency
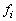 of the deflector are
defined by the following set of equations: of the deflector are
defined by the following set of equations:
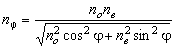 , , |
(3d) |
 , , |
(4d) |
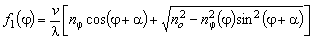 . . |
(5d) |
Eqs (4d) and (5d)
correspond to the geometry presented in Figs 1d 2d, respectively. Indices
of refraction for ordinary (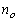 ) and extraordinary ( ) and extraordinary (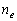 ) polarized beams are
determined with taking into account their dispersive dependence. ) polarized beams are
determined with taking into account their dispersive dependence.
The
sound velocity v depends on the angle 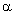 as as
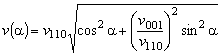 , , |
(6d) |
where 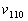 and and 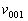 are the sound velocities
along the axes [110] and [001], correspondingly. The value are the sound velocities
along the axes [110] and [001], correspondingly. The value  is determined by the
angles is determined by the
angles 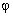 and and 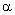
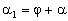 . . |
(7d) |
The
wedge angle 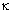 can be found from
the expression can be found from
the expression
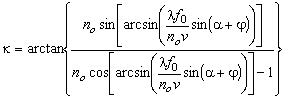 . . |
(8d) |
The
angle  is defined from the
formula is defined from the
formula
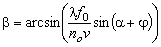 . . |
(9d) |
Here
we present characteristics of acoustooptic deflectors for major laser
wavelength 488 nm, 515 nm, 532 nm, 633 nm and 1064 nm, 1550 nm (Fig. 2d).
For the definition, we have chosen the central frequency 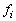 of all the deflectors
constant and equal to 80 MHz. The transducer length l
corresponds to the operating frequency band of the deflector equal to
35 MHz at 1.5 dB level. The transducer height is defined by the laser
beam diameter d. of all the deflectors
constant and equal to 80 MHz. The transducer length l
corresponds to the operating frequency band of the deflector equal to
35 MHz at 1.5 dB level. The transducer height is defined by the laser
beam diameter d.
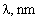 |
488
|
515
|
532
|
633
|
1064
|
1300
|
1550
|
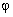 , deg. , deg. |
85.80
|
85.58
|
85.42
|
84.52
|
80.22
|
78.23
|
76.25
|
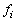 , MHz , MHz |
80
|
80
|
80
|
80
|
80
|
80
|
80
|
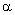 , deg. , deg. |
5.63
|
5.98
|
6.2
|
7.4
|
6.44
|
7.77
|
9.07
|
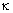 , deg. , deg. |
2.6
|
2.77
|
2.87
|
3.45
|
6.14
|
7.38
|
8.58
|
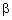 , deg. , deg. |
1.5
|
1.57
|
1.62
|
1.92
|
3.36
|
4.03
|
4.67
|
|
|